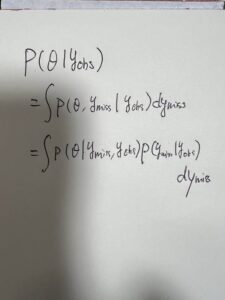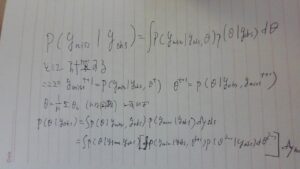①データの欠損は、入力ミス、無回答、システム上の問題など様々
取り扱いの問題は、無視するのか、除外するのか、尤もらしい値を入れるのか
を選ぶこと
リストワイズ削除>NaN行を全部削除
ペアワイズ削除>利用可能データのみを使う
Fillnaで埋める>欠損部を0にする
前値で埋める
平均値で埋める>平均値代入法
②欠損を含むデータが観測される確率は
p(y,l|θ、φ)
であらわされる
ここで
yは欠損データを含むデータをあらわし
lは欠損しているかどうかを表す情報
θはyの分布を表すパラメータで
φはlの分布を表すパラメータである
③multiple imputationはsingle imputationに対する意味ではなく
代入を繰り返すことで、EM アルゴリズムのようにパラメータを推定してゆく方法で
stochastic regression imputationにおいて何度も乱数生成を行うものではなく
まずI-STEPにおいて指定した分布から欠測値を補完し、
補完した結果からさらに確率分布のパラメータを推定する(P-STEP)
これらを繰り返すことで推定値を求めてゆく方法
欠損値を補完する際に複数の値を代入することから多重代入法と呼ばれる
④完全データをy
観測されたデータをyobs
欠損データをymissとする
知りたい目標は不完全データが与えられた下での
あるパラメータθが起こる確率値p(θ|yobs)である
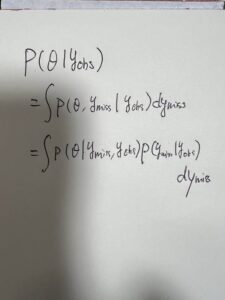
この積分は
p(ymis|yobs)を求めるために ymissで埋めた完全データを用いる
左辺のp(θ|yobs)はまた、1/D∑p(θ|ymiss, yobs)でもあるので
これらによりp(ymiss|yobs)を理論的には求めるのであるあが実際には困難なので下のようになる
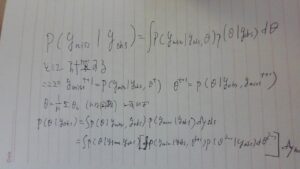
⑤EMアルゴリズムやMI法は
パラメータを推定する手順も含んだアルゴリズムである。
EMアルゴリズムは安定した性能が出ることが知られており
正規分布を仮定する場合には可能な計算量で計算できることが期待される
MI法はEM法とほぼ同じであるが欠損値のサンプリングが簡単にできる場合には高速化が期待できる
⑥Abstract
Because missing data are present in almost every study, it is important to handle missing data properly. First of all, the missing data mechanism should be considered. Missing data can be either completely at random (MCAR), at random (MAR), or not at random (MNAR). When missing data are MCAR, a complete case analysis can be valid. Also when missing data are MAR, in some situations a complete case analysis leads to valid results. However, in most situations, missing data imputation should be used. Regarding imputation methods, it is highly advised to use multiple imputations because multiple imputations lead to valid estimates including the uncertainty about the imputed values. When missing data are MNAR, also multiple imputations do not lead to valid results. A complication hereby is that it not possible to distinguish whether missing data are MAR or MNAR. Finally, it should be realized that preventing to have missing data is always better than the treatment of missing data.
1 Missing data mechanisms
Although researchers try to avoid missing data, these are present in almost every study. Ignoring missing data in statistical analysis can generate severely biased study results [
1]. Rubin [
2] was the first to develop a framework of different types of missing data (missing data mechanisms) that are important to determine the next steps in missing data handling. The three missing data mechanisms are missing completely at random (MCAR), missing at random (MAR), and missing not at random (MNAR). MCAR means that missing values are randomly distributed over the data sample. The reason for missing data is not related to relevant study variables or outcomes. For example, suppose a study in which people with familial hypertension are invited to come to the research center where blood pressure and several covariates are measured to investigate which covariates are related to blood pressure in this particular population. When data on blood pressure are missing, because some people were not able to visit the research center due to for instance a strike in public transport, these missing data are MCAR. MAR means that the probability of missing data is related to other variables. For example, when more data on blood pressure are missing of people with high body mass index, these missing data are MAR. MNAR is when the probability of missing data is dependent on the values of the variable itself. This is the case when people with the highest values for blood pressure do not visit the research center. This latter situation is problematic because you never know whether this is the case or not. When missing data are MNAR, there is no easy method to produce valid results. One possibility is to conduct several sensitivity analyses to study the influence of missing data on study outcomes [
3,
4]. It should be realized that the missing data mechanism is variable-dependent, that is, in one study, missing data on some of the variables can be MCAR, whereas for other variables missing data can be MAR or MNAR. Regarding the missing data mechanisms, it does not matter whether the particular variable with missing data is the outcome variable of the study or one of the covariates.
2 Exploring missing data
It should be realized that by definition, it is not possible to evaluate if the missing data are MAR or MNAR. The difference between the two is that when missing data are MNAR, missing data are related to unobserved data and because the data are unobserved and therefore unknown, it is impossible to evaluate whether the unobserved data are related to the missing data. There are, however, several possibilities to explore if the data are MCAR or not [
5,
6].
T-tests and logistic regression analyses can be used to investigate if there is a relationship between variables with and without missing data. The variable with missing data can be coded 0 for the observed and 1 for the missing data. When this variable (i.e., the missing data indicator variable) is used as a grouping variable in a
t-test or as an outcome in a logistic regression analysis, the relationship with other variables can be explored. Another method that can be used is Little's MCAR test.
3 Methods to deal with missing data
There are different methods available on how to deal with missing data [
7]. A method that is still commonly used is complete-case analysis (CCA), where all persons with missing values on one or more variables are excluded from the analysis. CCA has a lot of drawbacks and should be avoided in general [
8]. Only in some, even MAR missing data situations, CCA may generate unbiased results. For instance, when only outcome data are missing and the analysis is adjusted for variables related to the missing outcome, CCA leads to unbiased results [
9]. Furthermore, in longitudinal data analyses, when outcome data are missing in some of the repeated measures, an analysis on the available data will also provide valid results [
10].
One of the mostly used methods to deal with missing data is imputation (replacement of missing data by real values). Single imputation methods such as mean imputation, imputation based on linear regression, or for longitudinal data, last value/observation carried forward are not recommended because most of these methods lead to an artificial decreased standard deviation in the variables to be analysed and, therefore, result in too small standard errors [
7]. The recommended method is multiple imputation (MI) [
11,
12]. MI consists of three phases: imputation, analysis, and pooling. In the imputation phase, each missing value is replaced by several different values, which leads to multiple imputed datasets. The values used for imputation are derived from an imputation regression model. In this imputation regression model, variables that are related to the missing data and/or are correlated with the incomplete data variables (variables known as auxiliary variables) are used to ‘predict’ the missing value [
13]. Additional noise is added to the predicted (imputed) values which guarantees spread in the imputed values. One advice that is sometimes overlooked is that the outcome variable has to be part of the imputation model [
14]. Although several methods are available for generating the imputed values [
15], the Multivariate Imputation by Chained Equations (MICE) procedure is mostly used and is implemented in standard software programs [
12]. Within MI predictive mean matching is the preferred method [
16]. Predictive mean matching uses observed values to impute missing values on basis of closest matches (nearest neighbors). This prevents the imputation of unrealistic values [
16]. In the MI analysis phase, the different datasets are analyzed with the appropriate statistical method and in the pooling phase, the results are summarized into one final estimate as per Rubin's rules. The uncertainty about the missing data is reflected in the standard error of the pooled effect estimate [
11].
As the imputation model is very important in MI, guidelines of how to specify it are available [
12,
16]. Furthermore, the implementation of postestimation pooling procedures for regression models and procedures as chi-squared and likelihood ratio tests [
17] are increasingly developed for R software and can be found in packages as mice [
18], miceafter [
19], miceadds [
20], and psfmi [
21].
4 To impute or not to impute
Table 1 gives a summary whether imputation is necessary and which imputation method should be used. First of all, it should be realized that when data are MCAR, complete case analysis is a less precise but still valid way to analyse the data. It is sometimes argued that also in MCAR situations, imputation should be used to increase the power of the analysis. That is a weak argument and should not be used in general to perform missing data imputation. As in all statistical methods, there are some guidelines about the percentage of missing data above which imputation is necessary. Mostly a missing data percentage of 5% is mentioned as a sort of cutoff. However, it should be realized that not only the percentage of missing data is important but also the strength of the relationship between missing and observed variables is important. Furthermore, it is suggested that MI can be used (or has to be used) even in situations with more than 50% missing data. However, when 50% or more of a particular variable is missing, it is highly questionable whether the available data of that particular variable are valid. In situations like that, it is maybe better to leave that particular variable out of the analyses. That does not have to be a big problem because in all studies some important variables are not measured at all.
5 Final remarks
Research on MI is ongoing and focuses currently among others on the development of imputation models for multilevel data [
22,
23], questionnaire data [
24,
25], cost-effectiveness data [
26], and the development and validation of prognostic models [
27,
28]. As missing data can seriously influence study outcome, they have to be well addressed. Guidelines on how to conduct a suitable missing value analysis and to choose a proper method to handle the missing data are currently within reach of every researcher [
29–31]. There is therefore no excuse anymore to ignore missing data.
6 Key issues
•
Regarding missing data, prevention is always better than treatment.
•
When missing data are MCAR, complete case analysis may be valid.
•
Single imputation methods lead to underestimated standard error of the effect estimates.
•
MI is only valid when missing data are MAR.
•
It is not possible to evaluate if the missing data are MAR or MNAR.
7 Suggestions for further reading
Buuren, S.V. (2018), Flexible Imputation of Missing Data (second edition), and Chapman and Hall/CRC provides practical information and R code of the application of the MICE procedure.
White I.R., Royston P., Wood A.M. Multiple imputation using chained equations: Issues and guidance for practice. Stat Med. 2011 February 20; 30(4):377-99. Provides a lot of practical advice when applying MI.
Lee K.J., Tilling K.M., Cornish R.P., Little R.J.A., Bell M.L., Goetghebeur E., Hogan J.W., Carpenter J.R.; STRATOS initiative. Framework for the treatment and reporting of missing data in observational studies: The Treatment and Reporting of Missing data in Observational Studies framework. J Clin Epidemiol. 2021 June; 134:79-88. Presents a practical framework on how to handle and report missing data in observational studies.
Collins L.M., Schafer J.L., Kam C.M. A comparison of inclusive and restrictive strategies in modern missing data procedures. Psychol Methods 2001; 6(4):330-51. Classic paper about the importance of adding auxiliary variables to the imputation procedure.
Eekhout I., de Vet H.C., de Boer M.R., Twisk J.W., Heymans M.W. Passive imputation and parcel summaries are both valid to handle missing items in studies with many multi-item scales. Stat Methods Med Res. 2018 April; 27(4):1,128-1,140. Explains a procedure of how to handle missing data when various multi-item scales are used.
References
Schafer, J.L. ∙ Graham, J.W.
Missing data: our view of the state of the art
Psychol Methods. 2002;
7:147-177
Rubin, D.B.
Inference and missing data
Biometrika. 1976;
63:581-592
Héraud-Bousquet, V. ∙ Larsen, C. ∙ Carpenter, J. ...
Practical considerations for sensitivity analysis after multiple imputation applied to epidemiological studies with incomplete data
BMC Med Res Methodol. 2012;
12:73
Hsu, C.H. ∙ He, Y. ∙ Hu, C. ...
A multiple imputation-based sensitivity analysis approach for data subject to missing not at random
Stat Med. 2020;
39:3756-3771
Enders, C.K.
Applied missing data analysis
The Guilford Press, New York, NY, 2010
Heymans, M.W. ∙ Eekhout, I.
Applied missing data analysis with SPSS and RStudio
Available at
Eekhout, I. ∙ de Boer, R.M. ∙ Twisk, J.W. ...
Missing data: a systematic review of how they are reported and handled
Epidemiology. 2012;
23:729-732
Austin, P.C. ∙ White, I.R. ∙ Lee, D.S. ...
Missing data in clinical research: a tutorial on multiple imputation
Can J Cardiol. 2021;
37:1322-1331
Groenwold, R.H. ∙ Donders, A.R. ∙ Roes, K.C. ...
Dealing with missing outcome data in randomized trials and observational studies
Am J Epidemiol. 2012;
175:210-217
Twisk, J. ∙ de Boer, M. ∙ de Vente, W. ...
Multiple imputation of missing values was not necessary before performing a longitudinal mixed-model analysis
J Clin Epidemiol. 2013;
66:1022-1028
Rubin, D.B.
Multiple imputation for nonresponse in surveys
John Wiley & Sons, New York, 1987
Buuren, S.V.
Flexible imputation of missing data
Chapman and Hall/CRC, London, UK, 2018
Collins, L.M. ∙ Schafer, J.L. ∙ Kam, C.M.
A comparison of inclusive and restrictive strategies in modern missing data procedures
Psychol Methods. 2001;
6:330-351
Moons, K.G. ∙ Donders, R.A. ∙ Stijnen, T. ...
Using the outcome for imputation of missing predictor values was preferred
J Clin Epidemiol. 2006;
59:1092-1101
Lee, K.J. ∙ Carlin, J.B.
Multiple imputation for missing data: fully conditional specification versus multivariate normal imputation
Am J Epidemiol. 2010;
171:624-632
White, I.R. ∙ Royston, P. ∙ Wood, A.M.
Multiple imputation using chained equations: issues and guidance for practice
Stat Med. 2011;
30:377-399
Marshall, A. ∙ Altman, D.G. ∙ Holder, R.L. ...
Combining estimates of interest in prognostic modelling studies after multiple imputation: current practice and guidelines
BMC Med Res Methodol. 2009;
9:57
van Buuren, S. ∙ Groothuis-Oudshoorn, K.
Mice: multivariate imputation by chained equations in R
J Stat Softw. 2011;
45:1-67
Heymans, Martijn W.
Miceafter: data analysis and pooling after multiple imputation. R package version 0.1.0
Available at
Robitzsch, A. ∙ Grund, S.
Miceadds: some additional multiple imputation functions, especially for “mice”. R package version 3.11-6
Available at
Heymans, Martijn W.
Psfmi: prediction model pooling, selection and performance evaluation across multiply imputed datasets. R package version 1.0.0
Available at
Jolani, S. ∙ Debray, T.P. ∙ Koffijberg, H. ...
Imputation of systematically missing predictors in an individual participant data meta-analysis: a generalized approach using MICE
Stat Med. 2015;
34:1841-1863
Resche-Rigon, M. ∙ White, I.R.
Multiple imputation by chained equations for systematically and sporadically missing multilevel data
Stat Methods Med Res. 2018;
27:1634-1649
Eekhout, I. ∙ de Vet, H.C. ∙ Twisk, J.W. ...
Missing data in a multi-item instrument were best handled by multiple imputation at the item score level
J Clin Epidemiol. 2014;
67:335-342
Eekhout, I. ∙ de Vet, H.C. ∙ de Boer, M.R. ...
Passive imputation and parcel summaries are both valid to handle missing items in studies with many multi-item scales
Stat Methods Med Res. 2018;
27:1128-1140
Brand, J. ∙ van Buuren, S. ∙ le Cessie, S. ...
Combining multiple imputation and bootstrap in the analysis of cost-effectiveness trial data
Stat Med. 2019;
38:210-220
Austin, P.C. ∙ Lee, D.S. ∙ Ko, D.T. ...
Effect of variable selection strategy on the performance of prognostic models when using multiple imputation
Circ Cardiovasc Qual Outcomes. 2019;
12:e005927
Wahl, S. ∙ Boulesteix, A.L. ∙ Zierer, A. ...
Assessment of predictive performance in incomplete data by combining internal validation and multiple imputation
BMC Med Res Methodol. 2016;
16:144
Lee, K.J. ∙ Tilling, K.M. ∙ Cornish, R.P. ..., STRATOS Initiative
Framework for the treatment and reporting of missing data in observational studies: the treatment and reporting of missing data in observational studies framework
J Clin Epidemiol. 2021;
134:79-88
Little, R.J. ∙ D'Agostino, R. ∙ Cohen, M.L. ...
The prevention and treatment of missing data in clinical trials
N Engl J Med. 2012;
367:1355-1360
Sterne, J.A. ∙ White, I.R. ∙ Carlin, J.B. ...
Multiple imputation for missing data in epidemiological and clinical research: potential and pitfalls
BMJ. 2009;
338:b2393