多重補完法について
欠測値への対処方法は?
では欠測値が発生したとして、対処法や埋め方(補完方法)は?
大きく分けると3つほどあります。
- 単一補完(Single Imputation)
- 多重補完(Multiple Imputation)
- モデル解析(一般化線形混合モデル:Generalized Linear Mixed Model)
、最近の傾向では多重補完かモデル解析がいいとされています。
しかし、どんな方法でも「これがベスト」という方法はないことは前提であると理解しておきましょう。
なぜなら欠測じゃなかった時にどんな値だったか誰も知らないから。
欠測への対処方法には、強い仮定が入ります。
そのため、仮定をずらしても同じ解析結果が得られるのか、という感度解析を実施することがとても重要。
感度解析として実施した複数の解析で結論が同じになれば、例え欠測があったとしても頑健性のあるデータだったということを主張できます。
欠測値が何かを理解できたところで、多重代入法(Multiple Imputation)について解説していきます。
多重代入法の手順は、下記の4つ。
- 観測されているデータを基にして欠測データの事後分布を構築し、この事後分布からの無作為抽出を行って欠測を埋める。
- 1の手順で無作為に欠測を埋めたデータセットをM個(>1)用意する。
- M個のデータセットそれぞれに対して解析を実施する(M個の結果が得られる)
- M個の結果を適切な統合方法で1つに統合する(最終的に1つの結果が得られる)
この手順のイメージは、高橋先生・伊藤先生のこちらの論文の図2.1がわかりやすいです。
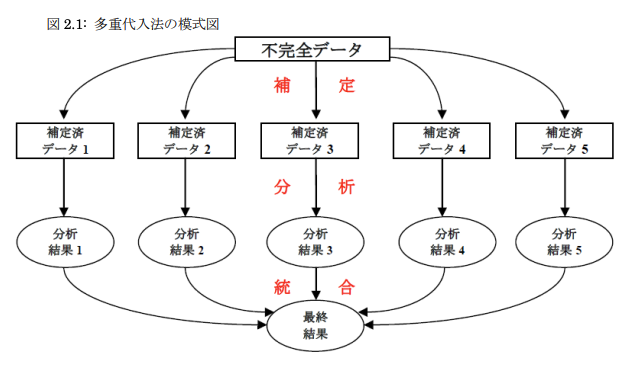
重要なのは「M個のデータセットそれぞれに対して解析を実施し、最後に統合する」という手順。
M個のデータセットの平均を計算して1つのデータセットにして1回の解析をする、という間違った手順で理解している方がいるので注意が必要です。
多重代入法では何個のデータセット作成が必要?
多重代入法としてM個のデータセットを作って解析し、最終的に統合することはわかりました。
じゃあMの具体的な数値はどれぐらいが適切なの?と疑問に思うかなと思います。
この疑問に対しても、高橋先生・伊藤先生のこちらの論文がわかりやすいです。
- 概ね 5~10 では少なすぎ、20~50 程度が適切だと考えられる。
- 欠測率に応じて「20%未満ならば M =20」「20%~30%ならば M = 30」「30%~40%ならば M = 40」「40%~50%ならば M = 50」といった具合に設定することが適切。
- 欠測率に関わらず、M = 100 を超えて得られるものは非常に少ない。
- たとえ M 数を数百まで拡大したとしても、補定値の精度を保証できなくなるおそれがある。
実際の論文ではどう設定しているのかをみると、例えば以下の論文ではM=20に設定されていることがわかります。

(参考:Multicenter Trial of a Combination Probiotic for Children with Gastroenteritis (Stephen B. Freedman et al., November 22, 2018, N Engl J Med 2018;379:2015-26.))
そのため、総合的に考えると、常にM=50程度に設定しておけば問題なさそうかなと思います。
欠測値への対処方法1:単一補完(Single Imputation)
欠測値への対処方法として、まずは単一補完法があります。
単一補完とは「なにかしらの一つの値で補完する(欠測値を埋めてしまう)」という方法のこと。
例えば最も有名なのは、LOCF(Last Observation Carried Forward)ですかね。
これは、最後に得られたデータで欠測値を補完する、という方法のこと。
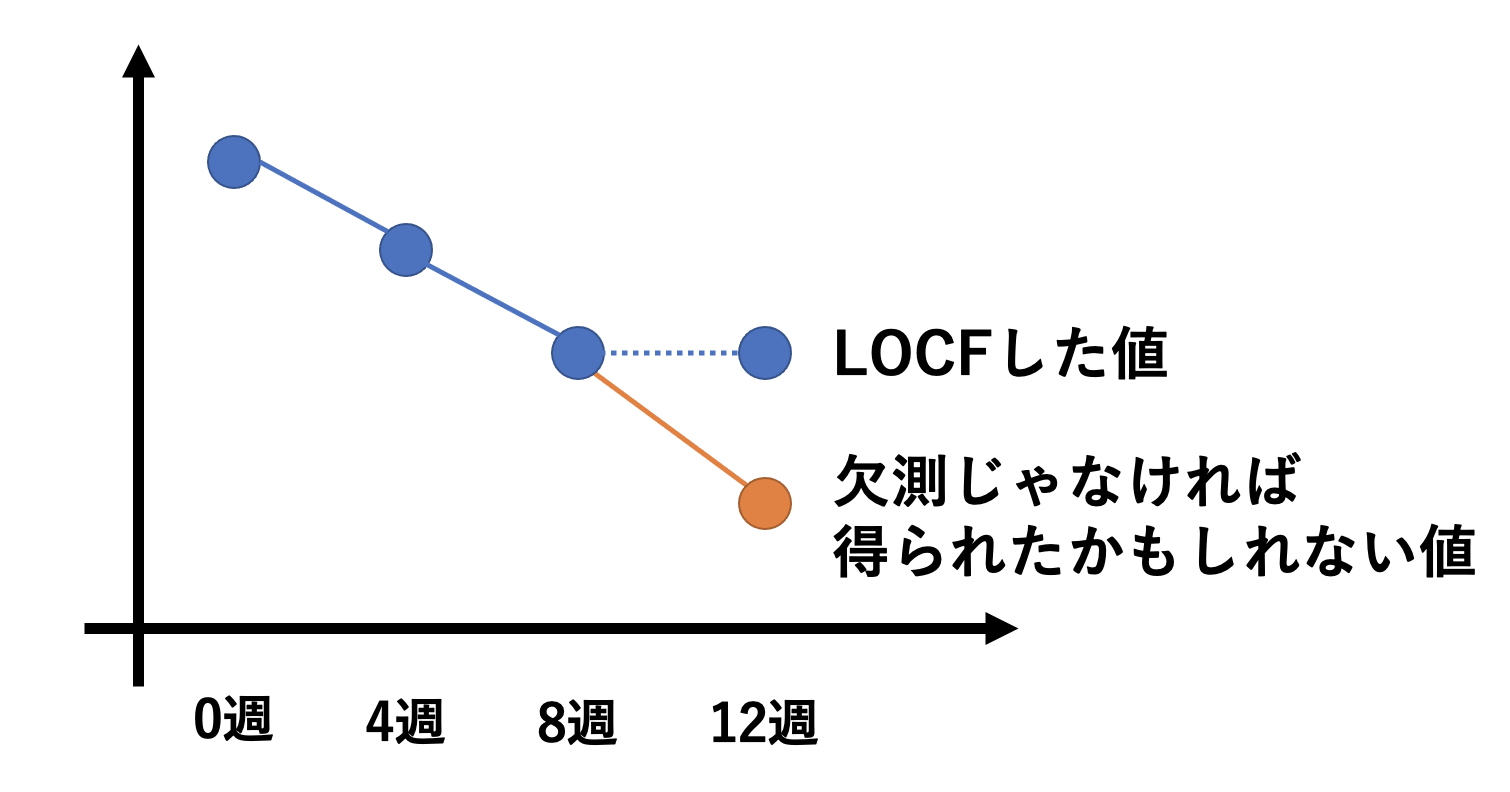
上記の通り、12週のデータが欠測だった場合には、最後に得られている8週のデータで補完してしまおう、というものですね。
しかしこの方法には強い仮定があります。
それは「最後に得られた値がそれ以降ずっと続く」という仮定。
本来、欠測じゃなければ得られたかもしれない値はもっと違うところにあったかもしれないですし、むしろその可能性の方が高いかもしれない。
そのため、欠測値が本来どのようなデータだったかは、誰も知らないので欠測への対処法にはかなり強い仮定が入るんだ、ということは理解しておいてください。
その他の単一補完法としては「ベストケースアナリシス」や「ワーストケースアナリシス」といったものがあります。
ベストケースアナリシスは、群間で一番差がつくように補完すること。
ワーストケースアナリシスは、群間で一番差がつかないように補完すること。
欠測値への対処方法2:多重補完(Multiple Imputation)
次の対処法は、多重補完法です。
先程の単一補完法は「一つのデータで埋めてしまう」という方法だったのですが、多重補完法はどういった方法でしょうか。
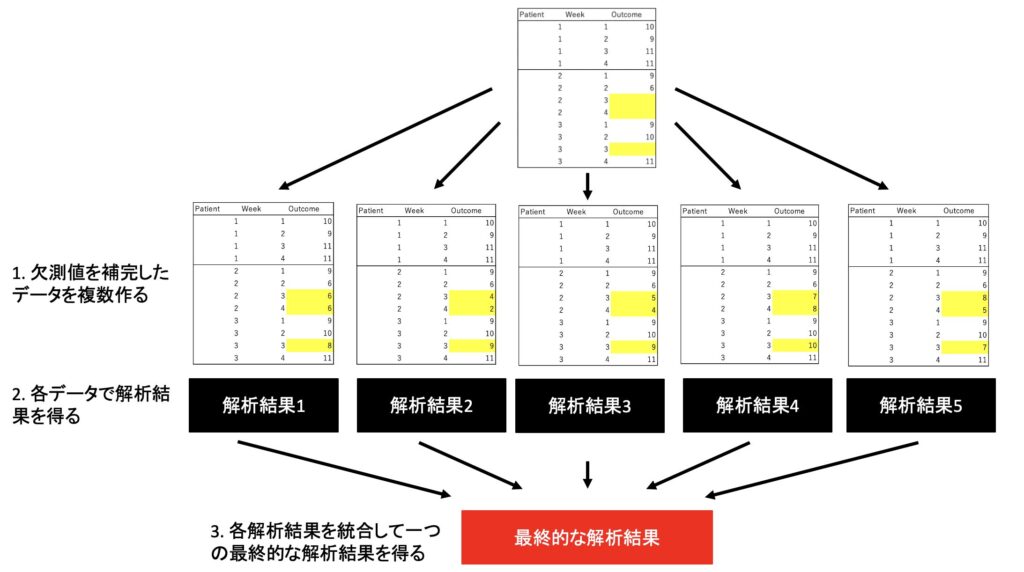
多重補完では以下の3つのことをやっています。
- 欠測値を代入したデータを複数個用意
- それぞれのデータに対して分析を実施
- 最終的にそれらの結果を統合して欠測値を補完
例えば、欠測値を補完した5個のデータを用意したとします。(5個じゃなくてもOK)
この時の補完方法は、乱数を使ったアルゴリズムに基づいた単一補完。
その5個に対して、やりたい解析を実施します。
すると解析結果が5個出てくるため、最終的にはそれを統合して1つの結果にしてしまいます。
欠測値への対処方法3:モデル解析(一般化線形混合モデル:Generalized Linear Mixed Model, MMRM)
最後に紹介するのが、モデル解析。
一般化線形混合モデル、と言われているものです。
特に連続変数(量的データ)に対してはMMRM(Mixed Model Reapeated Measure)というような解析手法として知られていますね。
一般化線型混合効果モデルは、被験者を変量効果として解析することで、個人個人の効果を統合して全体の効果を推定するイメージです。下記の図で、Aさんの時点4と時点5のデータが欠測だったとしても、Aさんの効果(直線)は推定でき、全体の効果も推定できるイメージです。
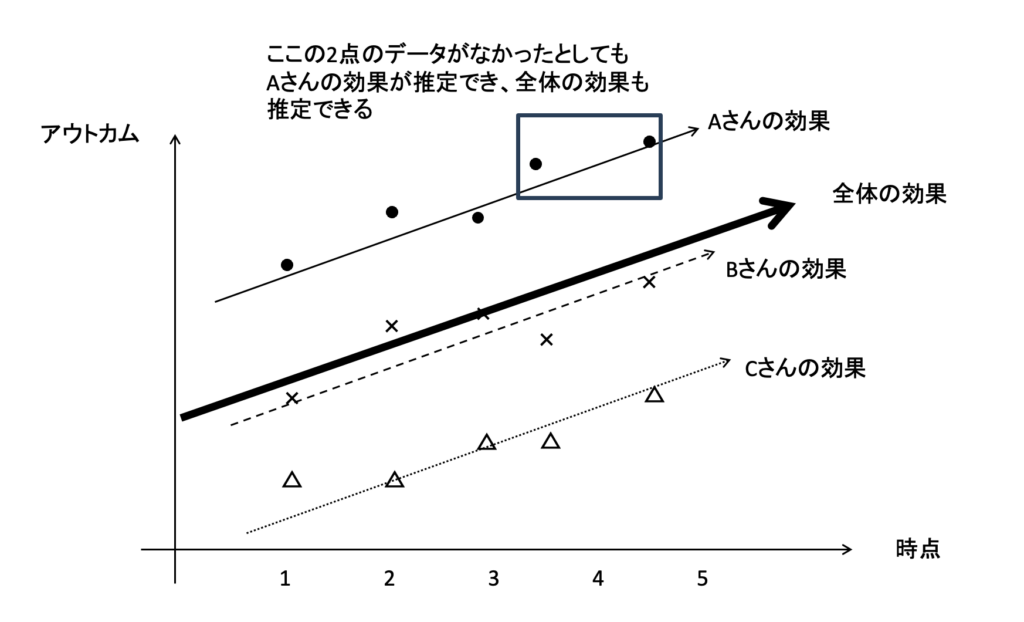
詳しいアルゴリズムなどは難しいので割愛しますが、理解しておいて頂きたいのは、この方法が欠測値を「補完」しているわけではないということ。
欠測値を考慮して解析はするが、あくまで補完法ではない、ということだけは理解しておきましょう。
欠測値(欠損値)への対処方法の大前提と論文への書き方は?
ここまで、欠測値に関して整理してきました。
そして、欠測値に対しての対処方法もお伝えしました。
では、欠測値が起こっても対処方法があるんだから、欠測値はどうとでもなるし安心だ、と思ったら注意です!
なぜなら、欠測値への対処方法としてはどんな方法でも「これがベスト」という方法はないから。
冒頭でもお伝えしましたが、欠測じゃなかった時にどんな値だったか誰も知らないから、どれが対処方法として正解かもわからない。
そして欠測への対処方法には、強い仮定が入ることもお伝えしました。
そのため、仮定をずらしても同じ解析結果が得られるのか、という感度解析を実施することがとても重要。
感度解析として実施した複数の解析で結論が同じになれば、例え欠測があったとしても頑健性のあるデータだったということを主張できます。
欠測値(欠損値)に対して論文への書き方は?
ありとあらゆる臨床研究で欠測値は生じうるものです。
むしろ欠測値がない臨床研究は存在するのか?と思うほど、欠測値はとても身近なものです。
そのため、論文へも欠測値へどのように対処したのかを記載していく必要があります。
例えば下記の論文を参考にしてみましょう。

(引用:https://evidence.nejm.org/doi/full/10.1056/EVIDoa2200097)
この論文のMethodを見ると、欠測値に関してかなり詳細に記載されております。
We assumed missing data to be missing at random and used multiple imputation by chained equations to impute missing data.
まずメインとなる欠測値への対処は、Missing at Random(MAR)を仮定して、多重補完法を実施した、ということが記載されております。
その次に、下記の記載もあります。
As a sensitivity analysis, we first performed our primary analysis (ANCOVA) using complete case data. In addition, we modeled our complete case data using a linear mixed model with LVEF as a continuous outcome, with treatment group and visit included as fixed effects and random intercepts by patient.
つまり、「コンプリートケース解析(欠測値を除外した解析)」と「MMRM(混合効果モデル)」を使った解析の2つを、感度解析として用いていることがわかります。
このように、「メインとなる欠測値への対処」と「感度解析」の2つを実施し、それを論文に報告することが重要になります!
まとめ
いかがでしたか?
この記事では「欠測値(欠損値)とは?埋め方(補完方法)や対処法はある?」ということでお伝えしました。
- そもそも欠測値(欠損値)とは?
- 欠測値の原因やメカニズムは?
- 欠測値の埋め方(補完方法)や対処法はある?
といったことが理解できたのなら幸いです!
こちらの内容は動画でもお伝えしていますので、併せてご確認くださいませ。
1.欠測のメカニズムと多重補完法(multiple imputation)
1.欠測のメカニズム
欠損値がどのようなメカニズムで欠測しているか、そしてどんな場合に多重補完が適した方法なのか、という理論的な解説を少しだけしておきましょう.
- missing completely at random(MCAR):欠測値が完全にランダムに発生している場合
- missing at random(MAR):欠損値の発生が完全にはランダムではないものの、欠損しているか否かが欠損値そのものに依存していない場合
- missing not at random (MNAR):欠損値の発生が欠損値そのものに依存する場合.例えば婚姻状態についての申告者の割合がもしかすると未婚者・既婚者・離婚者で異なるかもしれない場合はそのような欠測のメカニズムはこれに相当します.
これを実際の論文でどのように記載していくか、というのは難しい問題です.研究分野ごとの専門知識に従って推定するしかないと思います.
2.欠測値を補う方法
欠損値を含む症例を全部除外して分析する方法をcomplete-case analysis(CCA)といいます.Stataでは欠測値を含むデータを多変量解析に投入すると自動的に出てくる結果はこのCCAの結果になります.MCARの場合や欠損値を含む症例の割合が少ない場合、完全ケース分析は許容されますが、それ以外の場合では、完全ケース分析はデータの推計結果に歪みをもたらすため、何らかの対処が必要とされます.
1つの対処方法として、「欠損値」という新たなカテゴリーを作ってモデルに組み込む方法がありますが、「欠損値」カテゴリーにおける推定値の解釈が困難です.
それ以外の方法としては、欠損値に何らかの数値を代入し、欠損値を補完する方法があります.
- 1)平均値代入法(mean imputation)
- 2)回帰代入法(regression imputation)
- 3)last observation carried forward(LOCF) など
しかし、いずれもデータの推計値に歪みが生じるため、推奨されません.そこで多重補完法(multiple imputation)の出番です.
ちなみに本来はMARにおいて多重補完法は適応すべきとされていますが、実際にはこのようなメカニズムは簡単に区別が付くわけではなく、しばしば妥当な方法としてこの多重補完法が採用され、解析を実施します.
3.多重補完法のポイント
- 多重補完法はシミュレーションを利用したモデル推定の手法であり、欠損値を復元するものではない
- 代入モデルが適切、かつ解析モデルが適切という強い仮定が必要
- 代入回数は5-20回が適切と言われるが、その目安となるような指標も後述する
以上のようなポイントがあります.
2.multiple imputationにおいて入れるべき因子
1.MIにはアウトカムをいれるべきなのか
では実際にどんな因子を多重補完においては投入すべきなのでしょうか.結論から言えば、「アウトカムも含めて全部」となります.以下参考文献です.
In principle, the imputation model should contain all variables that are included in the main analysis as well as those that may predict both the incomplete variable and its incompleteness. Most importantly, failure to include the outcome in the imputation model can weaken the apparent association between the outcome and the imputed covariate.
Furukawa et al. Statistical Methods in Medical Research 2017, Vol. 26(2) 707–723
根拠となった論文は、Moons KG, Donders RA, Stijnen T, et al. Using the outcome for imputation of missing predictor values was preferred. J Clin Epidemiol 2006; 59: 1092–1101. です.
2.生存時間分析のときは時間と打ち切りをモデルに入れるべき
(2021/2/27修正)
他の回帰モデルと同様、Cox回帰での多重補完においてもアウトカム変数を入れるべきとされています.方法は様々提案されているようです.
For Cox regression, it has been shown that an imputation model conditional on D and the cumulative baseline hazard H0(T) can lead to approximately valid results in the main analysis.
Furukawa et al. Statistical Methods in Medical Research 2017, Vol. 26(2) 707–723
より具体的に言及しているのがこちらです.
Nelson-Aalen estimate of the cumulative hazard to the survival time
White IR and Royston P. Imputing missing covariate values for the Cox model. Stat Med 2009; 28: 1982–1998.
現実的には、survival outcome としてT(時間)あるいはln(T) と D(打ち切り変数)を入れてもさほど結果はずれることはないのだそうです.
なお、このNelson-Aalen estimateについては算出方法が先日(2021/2/24)のLightstoneさんのWebinarで紹介されていましたので、そちらで実施されるのがより確実なのかもしれません.
具体的には、sts generate 新変数 = na とするとこの推定量が各症例において得られますのでこれを組み込めばよいということになります.
3.欠測の割合はどのくらいが妥当なのか?
欠測値の割合と推定の妥当性についてはよく知られている経験則として、全体の25%以上の欠測があるとよくないかもしれない、ということがあります.Applied Missing Data Analysisの本でもシミュレーションをしているところでは25%のデータを欠測させたりしています.
(Demirtas et al. An imputation strategy for incomplete longitudinal ordinal data. Stat Med. 2008 Sep 10;27(20):4086-93が根拠となっているようです.)
しかしながら、これに対しては、「欠測割合は気にしなくてよい」とする論文もあります(Journal of Clinical Epidemiology 110 (2019) 63-73).代入モデルに十分に情報が与えられれば、大きな欠測割合の変数に対してもMIでバイアス、効率性の改善がある、ということが述べられています.
もう少し詳しく説明すると、欠測割合だけでは不十分であり、fraction of missing informationという考え方のほうが便利とのことです.そして一つ一つの変数に対する回帰式が十分な説明力(ここではR2)を有しているとき、MIによるばらつきは最小化できる、ということのようです.
The proportion of missing data is a common measure of how much information has been lost because of missing values in a data set. However, it does not reflect the information retained by auxiliary variables. Alternative measures such as the fraction of missing information (FMI) may be more useful as a tool for determining potential efficiency gains from MI. The FMI is a parameter-specific measure that is able to quantify the loss of information due to missingness, while accounting for the amount of information retained by other variables within a data set.
P. Madley-Dowd et al. Journal of Clinical Epidemiology 2019
もっとも、ここでいうモデルのR2は一番小さくて0.36、大きくて0.92とかなので、実は結構厳しいんじゃないかな~などと思ったりします.このFMIという指標もイマイチよくわかりませんので、統計の先生と相談しながらやるのが安全、というのが今のところの個人的な意見です.
3.代入するアルゴリズムと変数の扱いについて
1.代入するアルゴリズムの選択方法(2021/2/27 追記)
最も簡単なのが線形回帰モデルに基づいた代入法です.これは欠損のある変数が①連続変数であって②正規分布するという仮定に基づいています.正規性が成り立たない場合にはバイアスが生じてしまいます.
ここで、その他にもある代入モデルも含めて何を選択したらよいのかをきちんと整理しておきたいと思います.これもStataのWebinarから仕入れたネタになります.
- モノトーンパターンかどうか(misstable nestedというコマンドで確認できる)
- 単一の変数の代入が必要か、複数の変数の代入が必要か
- 連続変数で正規性があるかどうか
最初にモノトーンパターンかどうかで分けるのは、モノトーンパターンだと計算が少なく楽だからです.しかし現実のデータではそこまでシンプルにはいかないようです.
単一の変数の場合には
①連続変数で正規分布ならmi impute regress
②正規分布でない場合には、その他(mi impute intreg, mi impute logit, mi impute mlogit, mi impute nbreg, mi impute ologit, mi impute pmm, mi impute poisson, mi impute truncreg)
複数の変数で代入が必要になった場合には
ベイズ統計を利用したデータ拡大アルゴリズム(mvn)もしくはchainedを用いることになります.
mi impute mvn を用いる場合には以下の条件が必要になります.
- 欠損データが連続変数で正規分布に従う
- MCMCを使うので代入実行後に収束判定に関する診断をする必要がある.(ベイズ統計についてはまた項を改めて説明したいと思います.)
2.MICEかMVNか?
恐らく最もポピュラーな方法の1つが、Multivariate imputation by chained equations (MICE)というものです.多変量欠測データのimputationを変数ごとに回帰モデルを作って繰り返す、というものです.回帰モデルはregression, logistic, multinomial logisticなどの中から適切なモデルを変数ごとに選択します.これはもう一つのよく使われる方法であるmultivariate normal regression (MVN)と比べて次の様な利点があります.
- MVNは正規分布する連続変数のみの代入に使うが、MICEは幅広くパラ・ノンパラ、バイナリー、その他カテゴリ変数につかえる
- 複数の変数で同時に欠測が生じているときにも多重補完が可能
MVNですと、0/1の変数もすべて連続値に置き換わりますし、マイナスの値すら取り得るためその後にlogistic 回帰を実行できないなどの問題が生じてしまいます.
MICEですと、問題としては、前提となる仮定として「各変数の欠測に対する補完モデルとして、欠測を補完したい変数以外の他のすべての変数によってお互いに説明可能」という強い仮定を必要とすること、「この仮定を満たせない場合に得られた最終的な推定値の分散が正しく推定できるか保証されていないこと」があります.非常に強い仮定で、MICEにおけるfully conditionally specifiedの仮定と言います.
とはいえ複数の変数の欠測に対処可能という柔軟性を持っているので、よく使用されている補完アルゴリズムの1つです.
それと非常に計算量が多く、時間がかかるということです.時間がかかった挙げ句に収束しない、というオチも経験しますので、時間に余裕を持ってスケジューリングしましょう(笑)
3.変数の扱い
基本的にはMIでは多変量正規分布を仮定しているため、正規分布でない連続変数については対数変換をするなど何らかの処理が必要になります.ただ正規性が崩れても大きな問題はないとも言われているようです.
また、交互作用を見るような状況では交互作用項もいれるとよいようです.
2024年12月20日 | カテゴリー:自然科学的基礎知識//物理学、統計学、有機化学、数学、英語 |






