正規分布とt分布
t分布と正規分布の違い
母平均の推定・検定でどのように使い分けるか
データの平均値を推定したり検定したりするときには、正規分布を用いた方法と、t分布を用いた方法があります。
問題の状況によって、正規分布を使うか、t分布を使うか、が決まります
t分布と正規分布を使い分ける基準
t分布と正規分布を使い分ける基準は、母分散がわかっているかどうかで判断します。
母分散がわかっているときは正規分布を使用し、母分散がわかっていないときはt分布を使用します。
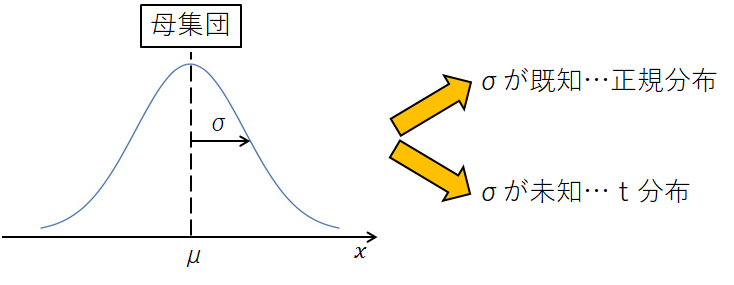
次節以降で、その理由と具体的な例を解説します。
t分布と正規分布を使い分ける理由
さきほどは、母分散が既知か未知かで使い分けることを説明しました。
実は、母分散が既知の場合でもt分布を使用することができます。
つまり、以下の表のように、t分布は母分散の既知・未知にかかわらず使うことができるのです。
| 母分散 | 正規分布を使った推定・検定 | t分布を使った推定・検定 |
|---|---|---|
| 既知 | 〇 | 〇 |
| 未知 | × | 〇 |
では、なぜ母分散が既知のときには正規分布を使うかというと、正規分布を使った方が推定・検定の精度がよいからです。
正規分布はt分布よりも尖った形状をしているので、同じ区間の幅が小さくなります。(下図)
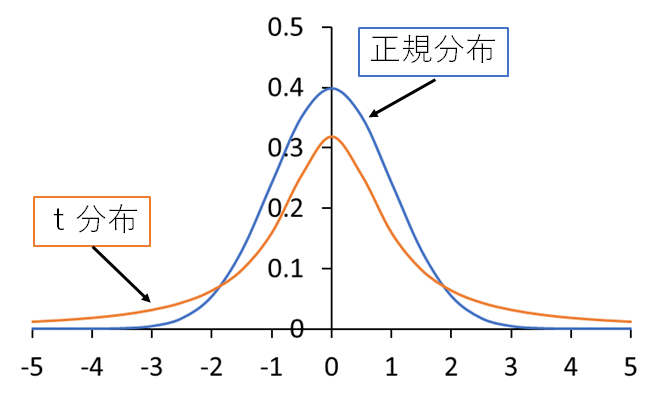
よって、母分散が既知のときには、推測の精度を上げるために正規分布を使う方がよいです。
母分散が既知のときの比較の例
母分散が既知のとき、正規分布を使った場合と、t分布を使った場合とで、推定結果にどのような違いがあるのかを例題で確認してみましょう。
正規分布にしたがう母集団から、データを 6個とった。
21, 20, 23, 20, 20, 19
長年の経験から、母分散は 1.9 であることがわかっている。
母平均の 95% 信頼区間を求めよ。
母分散がわかっていますので、正規分布を用いても、t分布を用いても解くことができます。
比較のために、両方で計算してみましょう。
正規分布の場合
6 個のデータの平均値は 20.5 ですので、母平均の 95% 信頼区間は、
母分散が 1.9 なので、σ=1.9−−−√ を代入して計算すると、
となります。
t分布の場合
6 個のデータの平均値は 20.5、不偏分散は 1.9 なので、95%信頼区間は、
不偏分散の値 s=1.9−−−√ を代入して
結果を見比べてみましょう。
母平均の 95%信頼区間は、
- 正規分布
[19.4,21.6] - t分布
[19.1,21.9]
正規分布の方が信頼区間の幅が小さく、推定には都合のよいことが分かります。
このように、母分散がわかっているときは正規分布を使うようにします
まとめ
結論としては、
- 母分散がわかっている(母分散既知)
正規分布を使う - 母分散がわかっていない(母分散未知)
t分布を使う
■検定統計量
身長や体重などについて検定を行う場合は、コインの裏表が出る確率とは異なり、取りうる値がどのくらいの確率でその値となるかが分かりません。そこで、身長や体重の値を「検定するための値」に変換します。このようにして算出された値が検定統計量(統計量と呼ばれることもあります)となります。
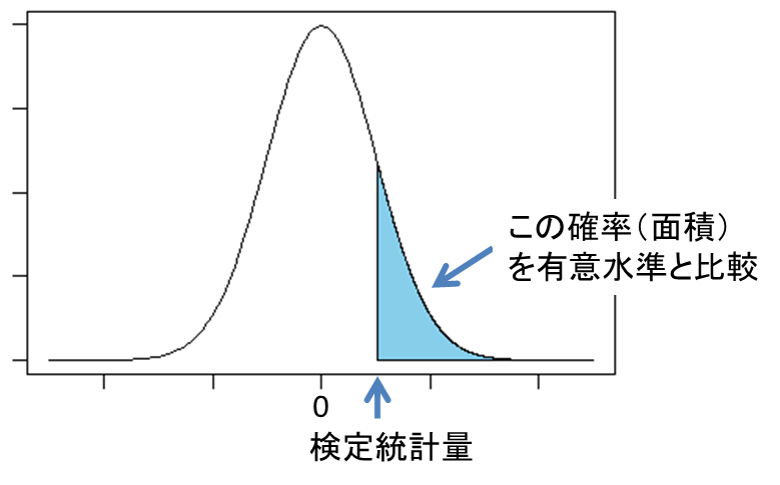
検定では、データから算出された検定統計量より極端な値をとる確率が有意水準と比較して大きいのか、小さいのかに基づいて帰無仮説を棄却するかどうかを判断します。検定統計量にはいくつかの種類がありますが、ここでは代表的な2つについて説明します。
1. 統計量z(=z値)
平均が0、分散が1となるようにデータを標準化した値のことです。例えば標本平均を標準化した値は次の式から算出できます(:データの平均、
:母平均、
:母分散、
:サンプルサイズ)。分母の
は標本平均の標準誤差=標本平均の標準偏差を表します。統計量zは標準正規分布に従うため、統計量zを用いた検定を行う際には標準正規分布を使います。
2. 統計量t(=t値)
20-1章で既に学びましたが、次の式から算出される値のことです(:不偏分散)。サンプルサイズがnの場合、統計量tは自由度
のt分布に従います。そのため、統計量tを用いた検定を行う際には自由度
のt分布を使います。統計量tを用いた検定のことを「t検定」といいます。t検定は、調べる値の母集団が正規分布することが前提条件となります。
例題:
日本人の男性100人をランダムに選び、その身長を測定したところ平均、不偏分散
となりました。身長の分布は正規分布に従うとする時、日本人の男性の平均身長は180cmと言ってよいでしょうか。
この場合の帰無仮説は「日本人の男性の平均身長は180cmである」、対立仮説
は「日本人の男性の平均身長は180cmではない」となります。この例題では母分散は分からないので、標本から得られた不偏分散
を使って統計量tを求めます。
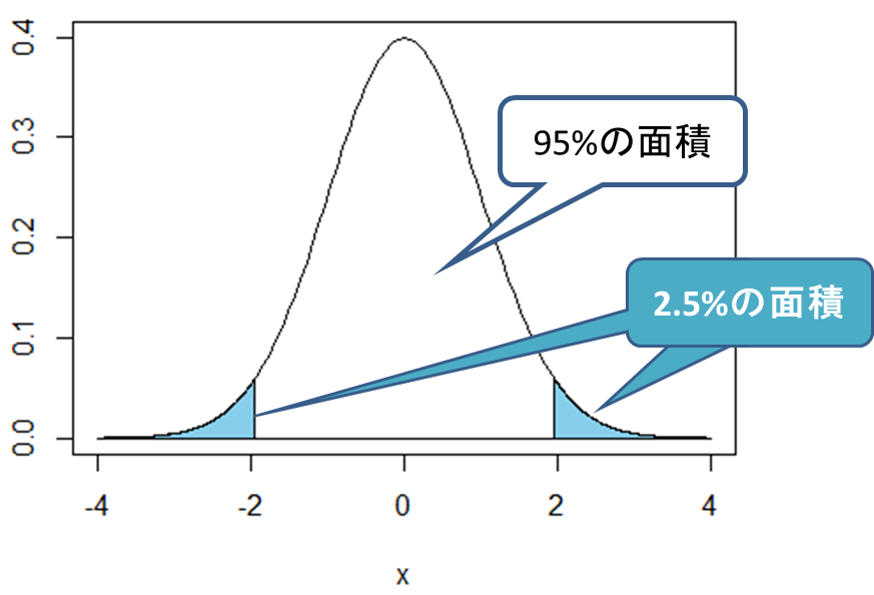
この統計量tを用いて検定を行います。有意水準5%で検定する時、統計量tが次の図のt分布の水色部分に入る場合に帰無仮説は棄却されます。両端の水色部分の面積は合わせると全体の5%であり、統計量tがこの部分に入るということは5%以下でしか起こらない極めて珍しい事象であると判定されます。
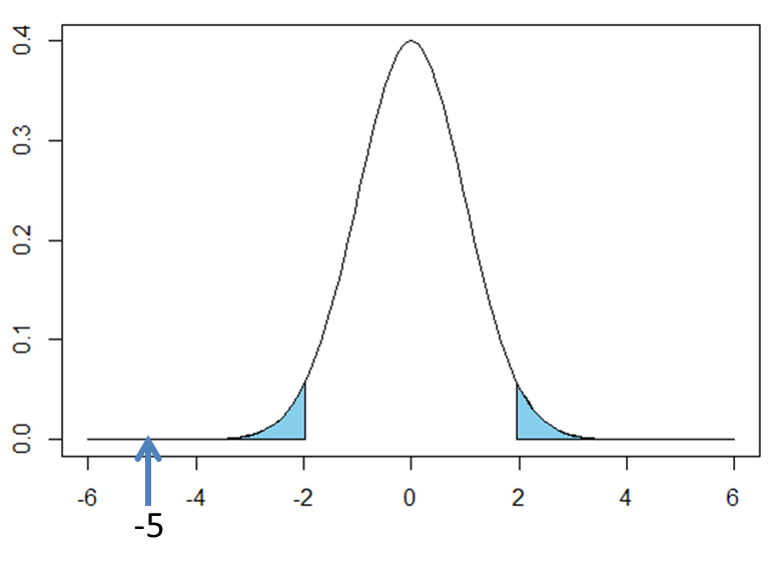
この例題では統計量t=-5となり、この値は上図の左側の水色部分に含まれるため、有意水準5%では帰無仮説は棄却され、対立仮説
が採択されます。つまり、「日本人の男性の平均身長は180cmではない」と結論づけられます。
■棄却域と採択域
上図の例で、水色の部分は帰無仮説が棄却される領域であることから「棄却域」と呼ばれます。反対に、白色の部分は帰無仮説
が棄却されない領域であることから「採択域」と呼ばれます。
2024年8月30日 | カテゴリー:基礎知識/物理学、統計学、有機化学、数学、英語 |





