ガンマ関数
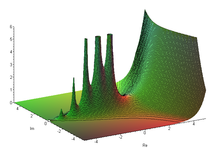
（グラフ中「Re」は x に相当、「Im」は y に相当）
（ガンマかんすう、英: gamma function）とは、数学において階乗の概念を複素数全体に拡張した特殊関数。複素階乗とも。一般に Γ(z) と表記される。
自然数 n に対しては、ガンマ関数と n の階乗との間では次の関係式が成り立つ：
- n!=Γ(n+1), Γ(n)=(n−1)!.
1729年に数学者レオンハルト・オイラーによって無限乗積の形で、最初に導入された[1]。Γ という記号は、1814年にルジャンドルが導入した[1]。また、それ以前にガウスが得ており Π などと表記していた（ただし、Π(z)=Γ(z+1) であった）。
定義
実部が正となる複素数 z に対して、次の広域積分で定義される複素関数：
- Γ(z)=∫0∞tz−1e−tdt(ℜz>0,)
をガンマ関数と呼ぶ[2]。この積分表示は第二種オイラー積分とも呼ばれる。
一般の複素数 z に対しては解析接続もしくは次の極限で定義される。
- Γ(z)=limn→∞nzn!∏k=0n(z+k).
他にも互いに同値となるいくつかの定義が存在する
基本的性質
0 または負の整数でない、かつ実部が正の任意の複素数 z に対して、
- Γ(z+1)=∫0∞e−ttzdt=[−e−ttz]0∞+z∫0∞e−ttz−1dt=zΓ(z)(∵[−e−ttz]0∞=0),
![{\displaystyle {\begin{aligned}\Gamma (z+1)&=\int _{0}^{\infty }e^{-t}t^{z}\,{\rm {d}}t\\&={\Bigl [}-e^{-t}t^{z}{\Bigr ]}_{0}^{\infty }+z\int _{0}^{\infty }e^{-t}t^{z-1}\,{\rm {d}}t\\&=z\Gamma (z)\qquad \left(\because {\Bigl [}-e^{-t}t^{z}{\Bigr ]}_{0}^{\infty }=0\right)\!,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11ee46dd4999406a1d95971915506839ecb211b2)
となることから、Γ(z+1)=zΓ(z) が成り立つ。またさらに、
- Γ(1)=∫0∞e−tdt=[−e−t]0∞=limt→∞(−e−t+1)=1,
![{\displaystyle {\begin{aligned}\Gamma (1)&=\int _{0}^{\infty }e^{-t}\,{\rm {d}}t={\Bigl [}-e^{-t}{\Bigr ]}_{0}^{\infty }=\lim _{t\to \infty }\!\left(-e^{-t}+1\right)\\&=1,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9960a09a00ac0836df78febf40ba717a29cbbd77)
である。これらの性質から、任意の正の整数 n に対して、
- Γ(n+1)=nΓ(n)=n(n−1)Γ(n−1)=⋯=n!Γ(1)=n!,
より Γ(n+1)=n! が成り立つ。その意味でガンマ関数は階乗の定義域を複素平面に拡張したものとなっている。
歴史的には、ガンマ関数は「階乗の複素数への拡張となるもの」（複素階乗）の実例として、オイラーにより考案された。階乗の複素数への拡張となる関数は無数に存在するが「正の実軸上で対数凸である解析関数」という条件を付ければ、それは一意に定まりガンマ関数に他ならない（ボーア・モレルップの定理）
定義の整合性
定義の積分表示と極限表示が一致することを示す。
Gn(z)=∫0ntz−1(1−tn)ndt
とすれば
- limn→∞(1−tn)n=e−t
であるから直感的には
- limn→∞Gn(z)=∫0∞tz−1e−tdt
である。（厳密にははさみうちの原理によって証明される）t = nu の置換により
Gn(z)=nz∫01uz−1(1−u)ndu
となる．nz を除く部分を gn(z) として
g0(z)=∫01uz−1du=[uzz]u=01=1z
gn(z)=∫01(uzz)′(1−u)ndu=nz∫u=01uz(1−u)n−1du=nzgn−1(z+1)
![{\displaystyle g_{0}(z)=\int _{0}^{1}{u^{z-1}}{\rm {d}}u=\left[{\frac {u^{z}}{z}}\right]_{u=0}^{1}={\frac {1}{z}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6a50b83c5f0b1fc1d74e5920340ea3198c60811)
これにより
Gn(z)=nzn!∏k=0n(z+k)
を得る。故に
∫0∞tz−1e−t dt=limn→∞Gn(z)=limn→∞nzn!∏k=0n(z+k)
である。
2024年8月14日 | カテゴリー：基礎知識/物理学、統計学、有機化学、数学、英語 |
